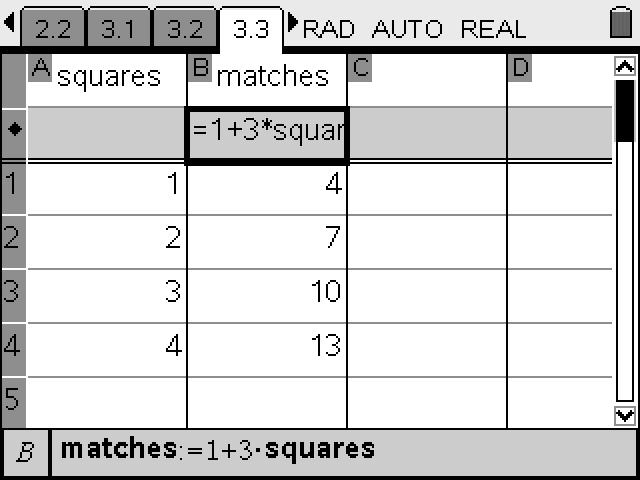
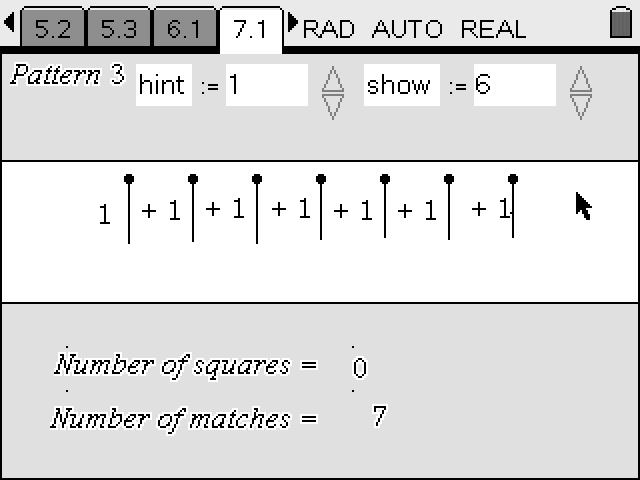
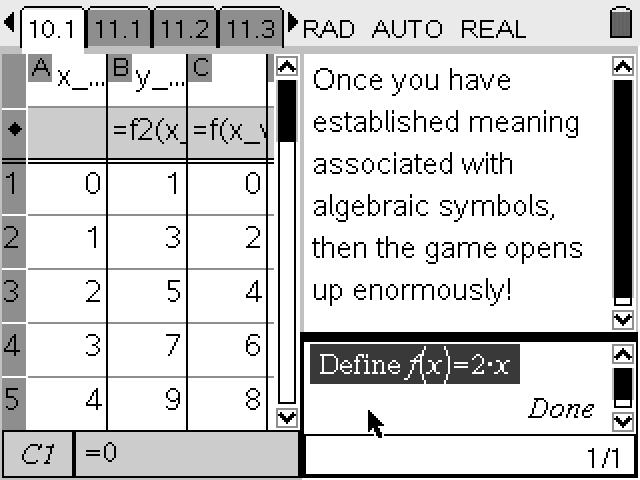
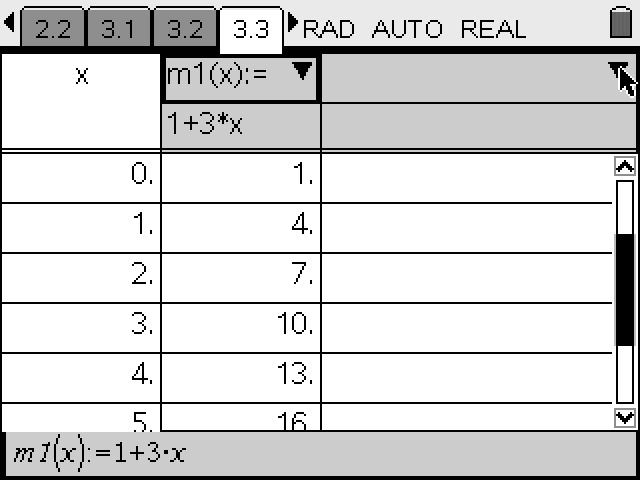
I began my career as an educator thirty years ago, and
since that time have taught mathematics, science and a range of other
subjects to students at all levels, from the Primary years through to
University and trainee teachers. At the same time that I was beginning my
teaching career, another newcomer was taking its first steps into
classrooms: I am referring here to computer-based technologies. I clearly
remember being charged with the task of buying the school's first computer
and "bringing us into the computer age"! Since that time, much has changed -
but much has also stayed the same, especially in mathematics classrooms at
all levels. Wherever we are in the world, one of the great constants has
tended to be in this domain. A study, several years ago, which asked
participants from many different countries to "Describe a typical
mathematics lesson" found surprisingly similar responses from the majority
of participants - responses which would have remained largely unchanged if
this same question had been asked forty or even fifty years earlier. While
many teachers and students are taking full advantage of the wonderful
teaching and learning tools now made possible by technology, the vast
majority, it would seem, remain firmly fixed in the old ways of doing
things. And it may be the domain of algebra that, for a variety of reasons,
has been most resistant to curricular and pedagogical change in response to
new technologies.
So what, if anything, have we learned from thirty years of classroom access
to computer-based technologies? What have we learned about good teaching and
learning in general? What have we learned about best practice in
mathematics? And what about the teaching and learning of algebra in
particular? And where does the use of open-ended mathematical software tools
(and especially computer algebra systems) fit into this pedagogy?
The answer is, in fact, that we have learned quite a lot about how students
learn and how teachers may most effectively teach. Research and the wisdom
of practice over the past three decades has done much to inform us with
regard to pedagogy and curricular approaches that are likely to be
effective.
My purpose here is to pose and then consider responses to several important
questions:
For many years (decades? centuries? millennia?), mathematics has been taught
as an arcane induction into mysteries that are revealed to the young by
those who have passed the initiation rites themselves. If previous
generations were successful in their learning of algebra using a syntactic
approach, then perhaps this is the way it is meant to be? After all, it
worked just fine for us, didn't it?
There are several problems with this line of argument, commonly heard in
staff rooms, around dinner tables, and on talk-back radio and television
current affairs shows. It holds up the values and practices of previous
generations as, if not ideal, then at least highly effective and challenges
new approaches as undermining and lowering what are generally perceived as
previously high standards. Conservatives and educational rationalists cite
increasing problems in schools and decreasing effectiveness of learning,
especially as evidenced in public examination results.
Part of the problem with this line of reasoning lies in biased perceptions
based on flawed memories: you are talking to a room full of middle-aged
mathematics teachers who blame the ready availability of calculators upon
the decrease in number skills, and remind everyone who will listen that we
did not need calculators - we
knew our tables, we learned our
fraction rules, we could perform long multiplication and long division by
hand.
What is missing in this argument is the recognition that, if we are trained
as mathematics teachers (or science, or language, or any professional
career) then
we were the few: we were the chosen. We were
the relatively small portion of our cohort who pulled this feat off.
What is forgotten from the "good old days" is that those who did not succeed
as we did were readily "streamed" into other classes, where we had little
more to do with them. Our cohort became more and more exclusive as we
progressed through high school and our numbers fewer. So when we reflect
back and remember that "most" of our cohort knew their tables and achieved
well, it is a small slice of the real picture.
We might reflect, too, that this was a culture which valued physical
punishment and fear as effective motivators, and a general consensus that
success followed from quickly and unquestioningly following instructions -
such factors may well have been effective as inducements for learning, but
they no longer exist, and there will be no return to such a place.
We are now educating into the senior years of high school the vast majority
of our students: from perhaps 20% of students completing the final stages of
secondary education when I was in school, we now see much closer to 90%.
Hardly surprising to find students attempting senior mathematics subjects
who have not mastered their multiplication tables! We need to recognise this
reality, and ensure that we offer appropriate educational experiences to
this much broader cohort - there must remain the highest levels of
mathematical study available to the few, but there must also be offerings
that are practical and worthwhile for all students.
Be clear that this does not excuse poor pedagogical practice at the highest
level, with the excuse that "they can handle it"! Good teaching is good
teaching and all our students deserve the opportunity to learn in ways that
are meaningful, if such ways are even possible.
Taken together, these elements conspire to fuel the most dangerous myth of
all: that mathematics is different from all the other disciplines, that its
demands are far more specialised, and that it is right and just that most
students of mathematics will fall by the wayside, because
mathematics is for the few - the majority of people are just
not meant to "get" mathematics. This argument excuses generations of poor
pedagogy and places the blame, not upon teachers, textbooks and curriculum
writers who were unable to find ways to share and communicate their subject
effectively, but upon their students, who were too lazy, or too dumb, or
just not "cut out for algebra"!
As a result of research on effective classrooms, on
what constitutes quality pedagogical practice, upon learning styles (and
the particular needs of students in the middle years), it is possible to
make some fairly well-supported and sensible statements at this point in
time concerning good teaching and learning, the teaching and learning of
mathematics, and of algebra in particular. It is then possible to relate
these to the appropriate and effective use of technology for the learning
of algebra in a meaningful way.
Students learn best when they are
actively engaged in constructing meaning about content that is relevant,
worthwhile, integrated and connected to their world.
Students
learn mathematics best when
-
They are active participants in their learning, not
passive spectators;
-
They learn mathematics as integrated and meaningful,
not disjoint and arbitrary;
-
They learn mathematics within the context of
challenging and interesting applications.
Students learn
algebra best when
-
It is not presented as meaningless symbols
following arbitrary rules;
-
The understanding of algebra is based upon
concrete foundations, with opportunities for manipulation and
visualisation;
-
Algebra is presented as a vital tool for modeling
real-world applications.
If these are the criteria by which we should judge
our algebra classrooms, how many of us would be found wanting?
How might we offer meaningful
algebra?
Top of Page
If algebra is to be taught in an effective and
meaningful way, then it must be taught differently than has been the case
in general to this point. High school algebra is perhaps the clearest
example of the malaise which affects almost all of school mathematics. We
can scarcely claim to be successful in the teaching and learning of a
subject in which the vast majority of students, after studying the subject
for at least 11 years, leave school not only being unable to apply much of
what they have "learned" in any practical or realistic way to their lives,
but with an active and often virulent dislike of the subject. Even many of
our "success stories" may be very capable "technicians" but can scarcely
claim to have any deep mastery or understanding of this discipline. They
can make the moves and perform the manipulations, but do they really
understand what they are doing?
By most reasonable measures, it is fair to claim
that the teaching of mathematics in schools generally has been less than
successful. Some might say spectacularly unsuccessful!
We can identify two significant factors which have
contributed to this current state:
-
Much of school Mathematics is taught in a
decontextualised, fragmented way, with little connection to the lives of
students or to the world beyond the classroom and examination.
-
Much of school mathematics is taught in a socially
and intellectually isolated way, as a series of routines to be learned
rather than processes to be understood. It is algorithmic rather than
meaningful, for what is algorithm but a suspension of meaning, designed
to break learning down to a memorized series of steps. Efficient?
Perhaps. Meaningful? No.
So what might be done?
First, look for opportunities to teach school
mathematics within contexts that are rich in meaning and significance for
students, engaging them and encouraging them to interact both with the
mathematics and with their peers in the learning of that
mathematics.
Second, reward informal as well as formal
approaches to mathematical thinking. Encourage multiple representations
and multiple approaches to problems and to solutions. While algorithmic
approaches may be considered efficient in reaching a specified solution,
the cost of that efficiency has been high, since it robs students of the
opportunities to play with the mathematics they are seeking to learn, to
make mistakes (and to learn from those mistakes), and to explore
individually and with others in a co-operative learning
environment.
And the role of technology in the process?
Technology in mathematics and science learning
plays two major roles:
-
As a tool for REPRESENTATION, and
-
As a tool for MANIPULATION
Good technology supports students in building
skills and concepts by offering multiple pathways for viewing and for
approaching worthwhile tasks, and scaffolds them appropriately throughout
the learning process.
The potential role for CAS in this domain is
problematic. If the biggest single problem with the teaching of algebra in
schools has been an over-reliance on a syntactic approach, and computer
algebra software is a purely syntactic tool, then it is capable of doing
enormous damage, of further reinforcing and rewarding those approaches
that have been least successful. CAS is a power tool for learning. Think
of it like a chainsaw: place such a tool in the hands of the inexperienced
and ignorant, and the results are easily predicted. Similarly with the
power tools of learning technology, which may easily do more harm than
good unless used carefully, and with caution.
It is easy to find applications of CAS in the senior
years with high ability students. But is there a place for it in the early
years of high school? I would argue that, CAS alone, especially in the
formative years of algebra learning, is a crippled tool; but used together
with other representations, and much more is possible. Computer algebra
becomes part of a "complete mathematical toolkit", along with the graph
plotter, the table of values, interactive geometry and statistics tools.
Together these tools have the potential to bring mathematics to life in
the hands of students, to offer insights into the power and capabilities
of this most beautiful of disciplines, to bring the messy wonder of the
real world into the classroom in ways that are capable of informing
student understanding - a far cry from the piece of chalk and the
textbook.
Within the domain of algebra, it is possible, I
believe, to identify certain "golden rules" for meaningful learning, rules
based upon research, the wisdom of practice and the experiences of capable
and effective educators at all levels who have informed my own pedagogical
development.